什么是貪心算法

在分析和求解某個問題時，在每一步的計算選擇上都是最優(yōu)的或者最好的，通過這種方式期望最終的計算的結果也是最優(yōu)的。也就是說，算法通過先追求局部的最優(yōu)解，從而尋求整體的最優(yōu)解。

貪心算法的基本步驟：

1、首先定義問題，確定問題模型是不是適合使用貪心算法，即求解最值問題；

2、將求極值的問題進行拆解，然后對拆解后的每一個子問題進行求解，試圖獲得當前子問題的局部最優(yōu)解；

3、所有子問題的局部最優(yōu)解求解完成后，把這些局部最優(yōu)解進行匯總合并，得到最終全局的最優(yōu)解，那么這個最優(yōu)解就是整個問題的最優(yōu)解。

通過場景理解算法

概念性的算法描述可能大家都不太好理解，所以需要結合一些實際的場景來進行說明。這里以我們小時候的找零錢的例子來進行切入。雖然現在大家都用手機掃一掃進行支付，已經很久到沒碰過錢了，但是并不妨礙找零問題 可幫助我們形象的理解貪心算法的實現過程。

假設你是一家小賣店的老板，你有各種面值大小的零錢，如1塊錢、3塊錢、5塊錢。這個時候有個小朋友過來買東西，他要求你找的零錢要張數最小，這樣他的口袋才能裝得下。假設我們分別把零錢記為c[0]、c[1]、c[2] ......，小朋友拿來買零食的錢我們記為total。那么剛才說的小朋友希望獲得最少張數零錢的需求我們就可以把他轉化為一個編程求最優(yōu)解的問題，即給定總數total，求解最少需要幾個c相加的和等于給定的總數total。

例子1：

假設給定需要找的零錢為11，當前的零錢為1塊、3塊、5塊。

輸入：total=11，c[0]=1,c[1]=3,c[2]=5

輸出：3

問題分析

通過提取問題中的關鍵詞“最少”，我們可以明確此問題的實際上就是一個求解最值的問題，只要找到滿足條件的最小零錢張數就可以解決找回最少零錢的問題了。想要找到最小的零錢張數，我們最先想到的方法就是進行窮舉，列舉出來所有可能的滿足總數為11的零錢組合。如下圖所示，再在這些組合中找到使用零錢張數最少的組合再計算具體的張數，我們就可以獲得最終的答案了。但是這顯然不是一個好的解決思路。因為如果對應的total很大，我們窮舉的結果將會爆發(fā)性增長。

那有沒有更好的解決辦法呢？這時候我們就可以考慮下貪心算法的實現了，找到滿足要求的最小張數零錢。既然是找零錢，那么我們可以將問題轉換為找到滿足總數total的零錢最少需要幾個步驟，實際上就是將問題拆分到每次找零錢的小步驟中，而貪心算法的核心就是需要在每個小步驟中貪心尋求局部最優(yōu)解。因此在找零錢的每個步驟中，都需要找到該步驟中對應的最優(yōu)解零錢大小，接下來我們來一起看下貪心算法執(zhí)行過程。這里假設各個面值的零錢比較充足。

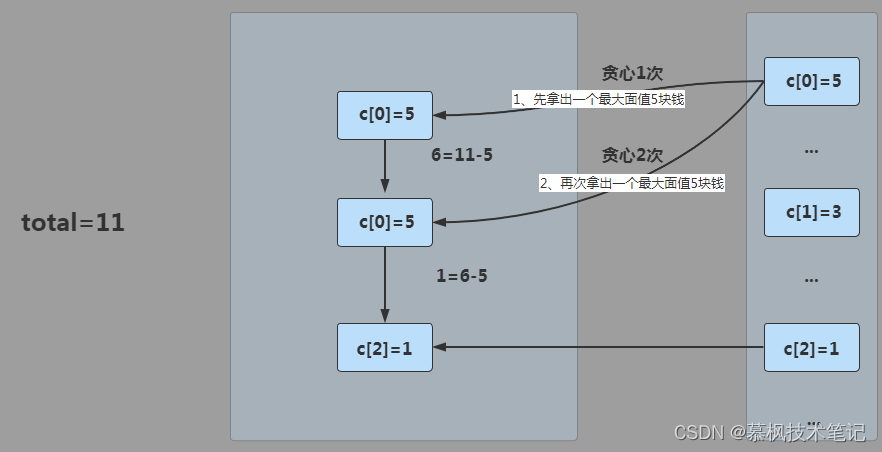
在尋找零錢的步驟中，首先獲取最大面值為5的零錢（貪心，上來就找最大的），接著發(fā)現剩余待找零錢6=11-5，于是繼續(xù)尋找最大的面值為5的零錢（繼續(xù)貪心），待找零錢1=6-5。此時只要獲取面值為1的零錢就可以完成任務了，再將之前步驟中的結果整合到一起，最終我們得出想要獲取total為11的最少張數零錢的大小為3。通過這樣的分析，貪心算法是不是也沒有那么的復雜。

對應的代碼實現如下所示：

 /**
 * @Author: mufeng
 * @Date: 2022/5/15 15:33
 * @Version: V 1.0.0
 * @Description: 計算最小滿足條件的零錢張數
 */
public class MinChangeCountSolution {
    public static void main(String[] args) {
        int values[] = {5,5,3,3,1};
        System.out.println(getMinChangeCount(11, values));
    }
    //假設values數組從大到小排列
    static int getMinChangeCount(int total, int[] values) {
        int rest = total;
        int result = 0;
        int count = values.length;
        // 從大到小遍歷所有面值
        for (int i = 0; i < count; ++ i) {
            //計算需要幾張這種面值的零錢
            int needCount = rest / values[i];
            //計算使用后的余額
            rest -= needCount * values[i];
            //計數增加
            result += needCount;
 
            if (rest == 0) {
                return result;
            }
        }
        //沒有找到合適的面值
        return -1;
    }
}

以上我們分析了貪心算法的大致實現過程，但是實際上還是有問題的。不知道大家有沒有發(fā)現，由于貪心算法過于貪心，每一個步驟都想要找到局部最優(yōu)解。那么假如在上面的例子中，我們沒有1塊錢的零錢，上述代碼的返回結果是-1，即沒有符合條件的答案。但是實際并非如此，也就是說5,3,3也是滿足條件的，但是上述代碼卻沒有找到。

所以上述代碼還是有問題的，關鍵點就在于，當發(fā)現沒有1元零錢的時候，需要回頭去看能不能把第二步驟中的5元零錢換成3元零錢再進行后續(xù)的迭代，如果有這樣的步驟，那么就可以找到5,3,3這樣的組合。

總結

本文主要通過對于貪心算法的描述，并結合實際的找零錢的例子，帶大家一起分析了貪心算法的具體實現過程。同時分析了貪心算法存在的不足，即容易陷入局部最優(yōu)的陷阱無法自拔，導致最終無法給出滿足條件的結果，這也是大家以后在使用貪心算法分析問題時特別需要注意的問題。

到此這篇關于Java貪心算法超詳細講解的文章就介紹到這了,更多相關Java貪心算法內容請搜索html5模板網以前的文章希望大家以后多多支持html5模板網！