簡介
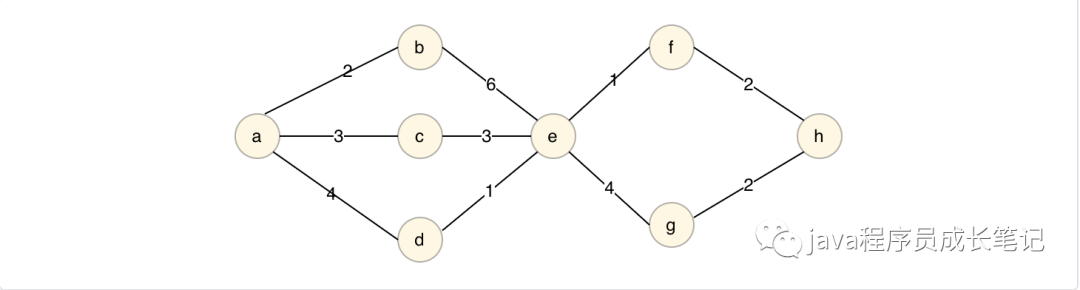
Dijkstra(迪杰斯特拉)算法是典型的單源最短路徑算法,用于計算一個節點到其他所有節點的最短路徑。主要特點是以起始點為中心向外層層擴展,直到擴展到終點為止。Dijkstra算法是很有代表性的最短路徑算法,在很多專業課程中都作為基本內容有詳細的介紹,如數據結構,圖論,運籌學等等。注意該算法要求圖中不存在負權邊。對應問題:在無向圖G=(V,E)中,假設每條邊E(i)的長度W(i),求由頂點V0到各節點的最短路徑。
工作過程
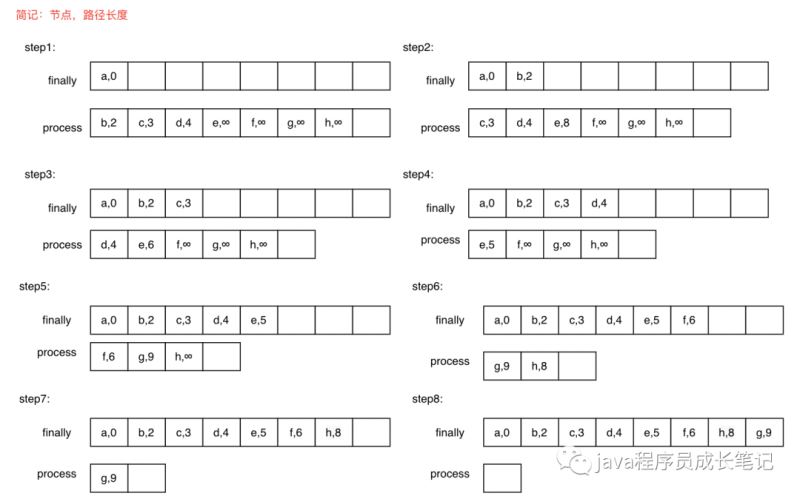
Dijkstra算法將頂點集合分為兩組,一組記錄已經求得最短路徑的頂點記為finallyNodes,一組正在求解中的頂點記為processNodes,step1:finallyNodes中頂點最開始只有源節點,最短路徑長度為0,而processNodes中包含除源節點以外的節點,并初始化路徑長度,與源節點直接相連的記路徑長度為權重,不相連的記為∞。step2:從process中選擇路徑長度最小的頂點,加入finallyNodes,并且更新processNodes,將與當前頂點相連的頂點路徑長度更新為min(當前權重,當前頂點最短路徑長度+當前頂點與頂點相連邊權重)。step3:重復step2,直至processNodes數組為空。
總體思路
這次我想先描述一下自己的大概思路,下面再寫具體實現。首先為了方便,我采用的是鄰接表存儲圖結構,鄰接表是一個二維數組,值存儲權重。根據上面工作過程中描述的內容,我們會有兩個中間集合記錄,finallyNodes記錄的是最終結果,我們只需要將計算的結果往里面塞即可。但是processNodes卻是一個不斷變化更新的集合,其中的操作包括刪除節點,更改節點值,查找節點值,同時我們每次需要拿出processNodes中記錄的距離最小的值,所以ProcessNodes準備用最小堆來做,那再刪除節點,更改節點值之后都需要調整堆為最小堆,java自帶的優先隊列沒有提供更改節點值的操作,因此我們這里需要自己實現一個小根堆,支持以上操作。然后就中規中矩實現dijkstra算法即可。
實現
小根堆
如果對堆不太熟悉的可以先看看這篇文章:堆(優先隊列),這里就不過多解釋了,直接貼代碼。這里堆中存的數據格式為int二維數組,存儲節點下標位置和對應距離,排序按存儲的距離進行排序。
public?class?MinHeap?{
? ? ? ?List<int[][]>?heap?;
? ? ? ?/**
? ? ? ??* 獲取并移除堆頂元素,并調整堆
? ? ? ??* @return
? ? ? ??*/
? ? ? ?public?int[][]?pop() {
? ? ? ? ? ?int[][]?top?=?heap.get(0);
? ? ? ? ? ?heap.set(0,?heap.get(heap.size()?-?1));
? ? ? ? ? ?heap.remove(heap.size()?-?1);
? ? ? ? ? ?//調整堆
? ? ? ? ? ?this.adjust(0,?heap.size()?-?1);
? ? ? ? ? ?return?top;
? ? ? }
? ? ? ?/**
? ? ? ??* 判斷是否為空
? ? ? ??* @return true/false
? ? ? ??*/
? ? ? ?public?boolean?isEmpty() {
? ? ? ? ? ?if?(null?==?this.heap) {
? ? ? ? ? ? ? ?return?true;
? ? ? ? ? }
? ? ? ? ? ?if?(this.heap.size()?==?0) {
? ? ? ? ? ? ? ?return?true;
? ? ? ? ? }
? ? ? ? ? ?return?false;
? ? ? }
? ? ? ?/**
? ? ? ??* 修改index位置節點的value值,并調整最小堆(Java priorityQueue未提供)
? ? ? ??* @param index 修改節點位置
? ? ? ??* @param value 修改值
? ? ? ??*/
? ? ? ?public?void?changeValue(int?index,?int?value) {
? ? ? ? ? ?int?src?=?heap.get(index)[0][1];
? ? ? ? ? ?heap.get(index)[0][1]?=?value;
? ? ? ? ? ?//直接比較當前值是變大還是變小,然后考慮是向上調整還是向下調整
? ? ? ? ? ?//則當前值可能往上移動
? ? ? ? ? ?if?(src?>?value) {
? ? ? ? ? ? ? ?this.upAdjust(index);
? ? ? ? ? ? ? ?return;
? ? ? ? ? }
? ? ? ? ? ?this.adjust(index,?heap.size()?-?1);
? ? ? }
? ? ? ?public?void?upAdjust(int?index) {
? ? ? ? ? ?//依次與雙親節點進行比較,小于雙親節點就直接交換。一直到根節點
? ? ? ? ? ?while?(index?>?0) {
? ? ? ? ? ? ? ?int?parent?=?index?>>?1;
? ? ? ? ? ? ? ?//雙親節點本來小于當前節點不需要進行調整
? ? ? ? ? ? ? ?if?(heap.get(parent)[0][1]?<=?heap.get(index)[0][1]) {
? ? ? ? ? ? ? ? ? ?break;
? ? ? ? ? ? ? }
? ? ? ? ? ? ? ?swap(index,?parent);
? ? ? ? ? ? ? ?index?=?parent;
? ? ? ? ? }
? ? ? }
? ? ? ?
? ? ? ?/**
? ? ? ??* 初始化一個最小堆
? ? ? ??* @param nums
? ? ? ??*/
? ? ? ?public?void?init(int[][]?nums) {
? ? ? ? ? ?heap?=?new?ArrayList<>(nums.length);
? ? ? ? ? ?for?(int?i?=?0?;?i?<?nums.length;?i?++) {
? ? ? ? ? ? ? ?int[][]?temp?=?new?int[1][2];
? ? ? ? ? ? ? ?temp[0][0]?=?nums[i][0];
? ? ? ? ? ? ? ?temp[0][1]?=?nums[i][1];
? ? ? ? ? ? ? ?heap.add(temp);
? ? ? ? ? }
? ? ? ? ? ?//從最后一個雙親節點開始將堆進行調整
? ? ? ? ? ?for?(int?i?=?nums.length?/?2?;?i?>=?0?;?--?i) {
? ? ? ? ? ? ? ?this.adjust(i,?nums.length?-?1);
? ? ? ? ? }
? ? ? }
? ? ? ?/**
? ? ? ??* 從當前index開始調節為最小堆
? ? ? ??* @param index 當前節點下標
? ? ? ??* @param end 最后一個節點下標
? ? ? ??*/
? ? ? ?private?void?adjust(int?index,?int?end) {
? ? ? ? ? ?//找到當前節點的孩子節點,將較小的節點與當前節點交換,一直往下,直至end
? ? ? ? ? ?while?(index?<=?end) {
? ? ? ? ? ? ? ?//左孩子節點
? ? ? ? ? ? ? ?int?left?=?index?<<?1;
? ? ? ? ? ? ? ?if?(left?+?1?<=?end?&&?heap.get(left?+?1)[0][1]?<?heap.get(left)[0][1] ) {
? ? ? ? ? ? ? ? ? ?//找到當前較小的節點
? ? ? ? ? ? ? ? ? ?++?left;
? ? ? ? ? ? ? }
? ? ? ? ? ? ? ?//沒有孩子節點,或者當前的孩子節點均已大于當前節點,已符合最小堆,不需要進行調整
? ? ? ? ? ? ? ?if?(left?>?end?||?heap.get(index)[0][1]?<=?heap.get(left)[0][1]) {
? ? ? ? ? ? ? ? ? ?break;
? ? ? ? ? ? ? }
? ? ? ? ? ? ? ?swap(index,?left);
? ? ? ? ? ? ? ?index?=?left;
? ? ? ? ? }
? ? ? }
? ? ? ?private?void?swap(int?i,?int?j) {
? ? ? ? ? ?int[][]?temp?=?heap.get(i);
? ? ? ? ? ?heap.set(i,?heap.get(j));
? ? ? ? ? ?heap.set(j,?temp);
? ? ? }
? }Dijsktra
數據結構
圖節點僅存儲節點值,一個Node數組nodes,存儲圖中所有節點,一個二維數組adjacencyMatrix,存儲圖中節點之間邊的權重,行和列下標與nodes數組下標對應。
//節點
Node[]?nodes;
//鄰接矩陣
int[][]?adjacencyMatrix;
public?class?Node?{
? ? ? ?private?char?value;
? ? ? ?Node(char?value) {
? ? ? ? ? ?this.value?=?value;
? ? ? }
? }初始化
初始化圖values標志的圖中所有節點值,edges標志圖中邊,數據格式為(node1的下標,node2的下標,邊權重)
private?void?initGraph(char[]?values,?String[]?edges) {
? ? ? ?nodes?=?new?Node[values.length];
//初始化node節點
? ? ? ?for?(int?i?=?0?;?i?<?values.length?;?i?++) {
? ? ? ? ? ?nodes[i]?=?new?Node(values[i]);
? ? ? }
? ? ? ?adjacencyMatrix?=?new?int[values.length][values.length];
//初始化鄰接表,同一個節點權重記為0,不相鄰節點權重記為Integer.MAX_VALUE
? ? ? ?for?(int?i?=?0?;?i?<?values.length?;?i++) {
? ? ? ? ? ?for?(int?j?=?0?;?j?<?values.length?;?j?++) {
? ? ? ? ? ? ? ?if?(i?==?j) {
? ? ? ? ? ? ? ? ? ?adjacencyMatrix[i][j]?=?0;
? ? ? ? ? ? ? ? ? ?continue;
? ? ? ? ? ? ? }
? ? ? ? ? ? ? ?adjacencyMatrix[i][j]?=?Integer.MAX_VALUE;
? ? ? ? ? ? ? ?adjacencyMatrix[j][i]?=?Integer.MAX_VALUE;
? ? ? ? ? }
? ? ? }
//根據edges更新相鄰節點權重值
? ? ? ?for?(String?edge?:?edges) {
? ? ? ? ? ?String[]?node?=?edge.split(",");
? ? ? ? ? ?int?i?=?Integer.valueOf(node[0]);
? ? ? ? ? ?int?j?=?Integer.valueOf(node[1]);
? ? ? ? ? ?int?weight?=?Integer.valueOf(node[2]);
? ? ? ? ? ?adjacencyMatrix[i][j]?=?weight;
? ? ? ? ? ?adjacencyMatrix[j][i]?=?weight;
? ? ? }
? ? ? ?visited?=?new?boolean[nodes.length];
? }初始化dijsktra算法必要的finallyNodes和processNodes
/**
* 標志對應下標節點是否已經處理,避免二次處理
*/
boolean[]?visited;
? ?/**
? ??* 記錄已經求得的最短路徑 finallyNodes[0][0]記錄node下標,finallyNodes[0][1]記錄最短路徑長度
? ??*/
? ?List<int[][]>?finallyNodes;
? ?/**
? ??* 記錄求解過程目前的路徑長度,因為每次取當前已知最短,所以最小堆進行記錄
? ??* 但是java優先隊列沒有實現改變值,這里需要自己實現
? ??* 首先每次取出堆頂元素之后,堆頂元素加入finallyNodes,此時需要更新與當前元素相鄰節點的路徑長度
? ??* 然后重新調整小根堆
? ??* 首先:只會更新變小的數據,所以從變小元素開始往上進行調整,或者直接調用調整方法,從堆頂往下進行調整
? ??*/
? ?MinHeap?processNodes;
/**
? ??* 初始化,主要初始化finallyNodes和processNodes,finallyNodes加入源節點,processNodes加入其他節點
? ??* @param nodeIndex
? ??*/
? ?private?void?initDijkstra(int?nodeIndex) {
? ? ? ?finallyNodes?=?new?ArrayList<>(nodes.length);
? ? ? ?processNodes?=?new?MinHeap();
? ? ? ?int[][]?node?=?new?int[1][2];
? ? ? ?node[0][0]?=?nodeIndex;
? ? ? ?node[0][1]?=?adjacencyMatrix[nodeIndex][nodeIndex];
? ? ? ?finallyNodes.add(node);
? ? ? ?visited[nodeIndex]?=?true;
? ? ? ?int[][]?process?=?new?int[nodes.length?-?1][2];
? ? ? ?int?j?=?0;
? ? ? ?for?(int?i?=?0?;?i?<?nodes.length?;?i++) {
? ? ? ? ? ?if?(i?==?nodeIndex) {
? ? ? ? ? ? ? ?continue;
? ? ? ? ? }
? ? ? ? ? ?process[j][0]?=?i;
? ? ? ? ? ?process[j][1]?=?adjacencyMatrix[nodeIndex][i];
? ? ? ? ? ?++?j;
? ? ? }
? ? ? ?//初始化最小堆
? ? ? ?processNodes.init(process);
? }dijsktra算法實現
public?void?dijkstra() {
? ? ? ?//1。堆頂取出最小元素,加入finallyNodes
//2。將與堆頂元素相連節點距離更新,
? ? ? ?while?(!processNodes.isEmpty()) {
? ? ? ? ? ?int[][]?head?=?processNodes.pop();
? ? ? ? ? ?finallyNodes.add(head);
? ? ? ? ? ?int?nodeIndex?=?head[0][0];
? ? ? ? ? ?visited[nodeIndex]?=?true;
? ? ? ? ? ?//跟堆頂元素相鄰的元素
? ? ? ? ? ?for?(int?j?=?0?;?j?<?nodes.length?;?j?++) {
? ? ? ? ? ? ? ?//找到相鄰節點
? ? ? ? ? ? ? ?if?(visited[j]?||?Integer.MAX_VALUE?==?adjacencyMatrix[nodeIndex][j]) {
? ? ? ? ? ? ? ? ? ?continue;
? ? ? ? ? ? ? }
? ? ? ? ? ? ? ?for?(int?i?=?0?;?i?<?processNodes.heap.size() ;?i++) {
? ? ? ? ? ? ? ? ? ?int[][]?node?=?processNodes.heap.get(i);
? ? ? ? ? ? ? ? ? ?//找到節點并且值變小,需要調整
? ? ? ? ? ? ? ? ? ?if?(node[0][0]?==?j?&&?node[0][1]?>?head[0][1]?+?adjacencyMatrix[nodeIndex][j]) {
? ? ? ? ? ? ? ? ? ? ? ?processNodes.changeValue(i,?head[0][1]?+?adjacencyMatrix[nodeIndex][j]);
? ? ? ? ? ? ? ? ? ? ? ?break;
? ? ? ? ? ? ? ? ? }
? ? ? ? ? ? ? }
? ? ? ? ? }
? ? ? }
? }測試
public?static?void?main(String[]?args) {
? ? ? ?char[]?values?=?new?char[]{'A','B','C','D','E','F','G','H'};
? ? ? ?String[]?edges?=?new?String[]{"0,1,2","0,2,3","0,3,4","1,4,6","2,4,3","3,4,1","4,5,1","4,6,4","5,7,2","6,7,2"};
? ? ? ?Dijkstra?dijkstra?=?new?Dijkstra();
? ? ? ?dijkstra.initGraph(values,?edges);
? ? ? ?int?startNodeIndex?=?0;
? ? ? ?dijkstra.initDijkstra(startNodeIndex);
? ? ? ?dijkstra.dijkstra();
? ? ? ?for?(int[][]?node?:?dijkstra.finallyNodes) {
? ? ? ? ? ?System.out.println(dijkstra.nodes[node[0][0]].value?+?"距離"?+?dijkstra.nodes[startNodeIndex].value?+?"最短路徑為:"?+?node[0][1]);
? ? ? }
? }
以上就是詳解Java中Dijkstra(迪杰斯特拉)算法的圖解與實現的詳細內容,更多關于Java Dijkstra算法的資料請關注html5模板網其它相關文章!
