為了方便起見,這些模型通常簡稱為TAR模型。這些模型捕獲了線性時間序列模型無法捕獲的行為,例如周期,幅度相關的頻率和跳躍現象。Tong和Lim(1980)使用閾值模型表明,該模型能夠發現黑子數據出現的不對稱周期性行為。
一階TAR模型的示例:
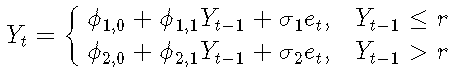
σ是噪聲標準偏差,Yt-1是閾值變量,r是閾值參數, {et}是具有零均值和單位方差的iid隨機變量序列。
每個線性子模型都稱為一個機制。上面是兩個機制的模型。
考慮以下簡單的一階TAR模型:
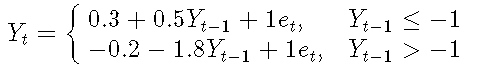
#低機制參數
i1 = 0.3
p1 = 0.5
s1 = 1
#高機制參數
i2 = -0.2
p2 = -1.8
s2 = 1
thresh = -1
delay = 1
#模擬數據
y=sim(n=100,Phi1=c(i1,p1),Phi2=c(i2,p2),p=1,d=delay,sigma1=s1,thd=thresh,sigma2=s2)$y
#繪制數據
plot(y=y,x=1:length(y),type='o',xlab='t',ylab=expression(Y[t])
abline(thresh,0,col="red")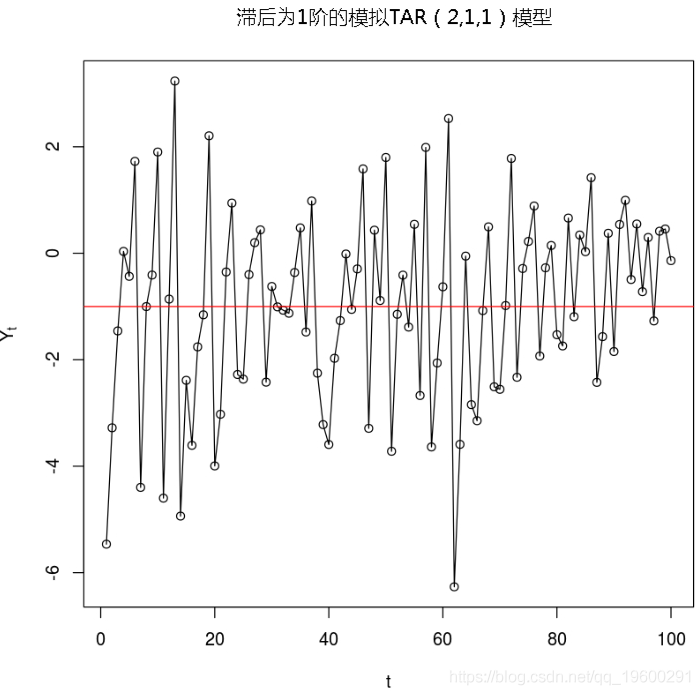
TAR模型框架是原始TAR模型的修改版本。它是通過抑制噪聲項和截距并將閾值設置為0來獲得的:
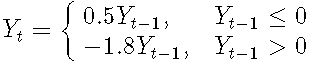
框架的穩定性以及某些規律性條件意味著TAR的平穩性。穩定性可以理解為,對于任何初始值Y1,框架都是有界過程。
在[164]中:
#使用不同的起點檢查穩定性
startvals = c(-2, -1.1,-0.5, 0.8, 1.2, 3.4)
count = 1
for (s in startvals) {
ysk[1
} else {
ysk[i] = -1.8*ysk[i-1]
}
count = count + 1
}
#繪制不同實現
matplot(t(x),type="l"
abline(0,0)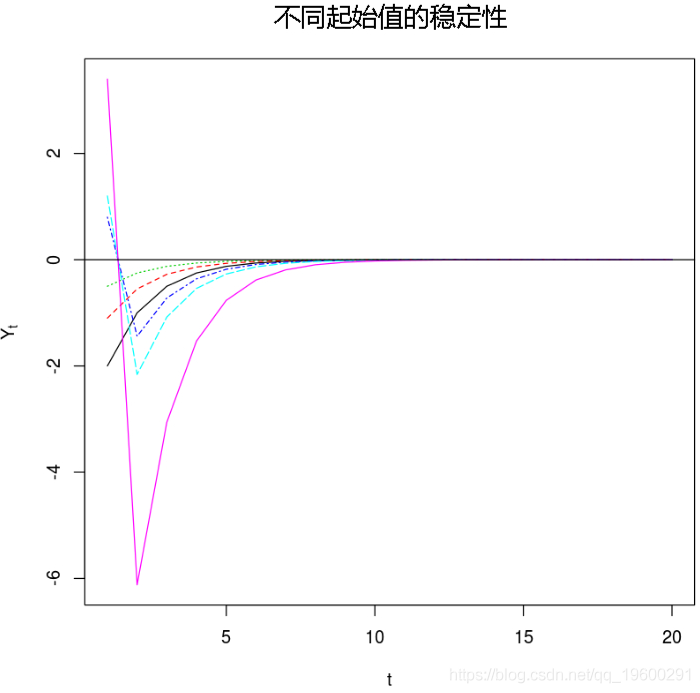
Chan和Tong(1985)證明,如果滿足以下條件,則一階TAR模型是平穩的
![]()
一般的兩機制模型寫為:
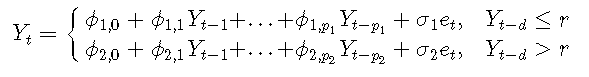
在這種情況下,穩定性更加復雜。然而,Chan and Tong(1985)證明,如果
![]()
模型估計
一種方法以及此處討論的方法是條件最小二乘(CLS)方法。
為簡單起見,除了假設p1 = p2 = p,1≤d≤p,還假設σ1=σ2=σ。然后可以將TAR模型方便地寫為
![]()
如果Yt-d> r,則I(Yt-d> r)= 1,否則為0。CLS最小化條件殘差平方和:
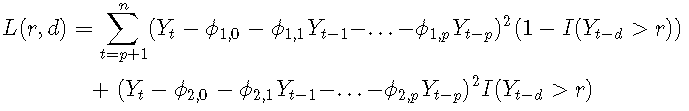
在這種情況下,可以根據是否Yt-d≤r將數據分為兩部分,然后執行OLS估計每個線性子模型的參數。
如果r未知。
在r值范圍內進行搜索,該值必須在時間序列的最小值和最大值之間,以確保該序列實際上超過閾值。然后從搜索中排除最高和最低10%的值
在此受限頻帶內,針對不同的r = yt值估算TAR模型。選擇r的值,使對應的回歸模型的殘差平方和最小。
#找到分位數
lq = quantile(y,0.10)
uq = quantile(y,0.90)
#繪制數據
plot(y=y,x=1:length(y),type='o',xlab='t'abline(lq,0,col="blue")
abline(uq,0,col="blue")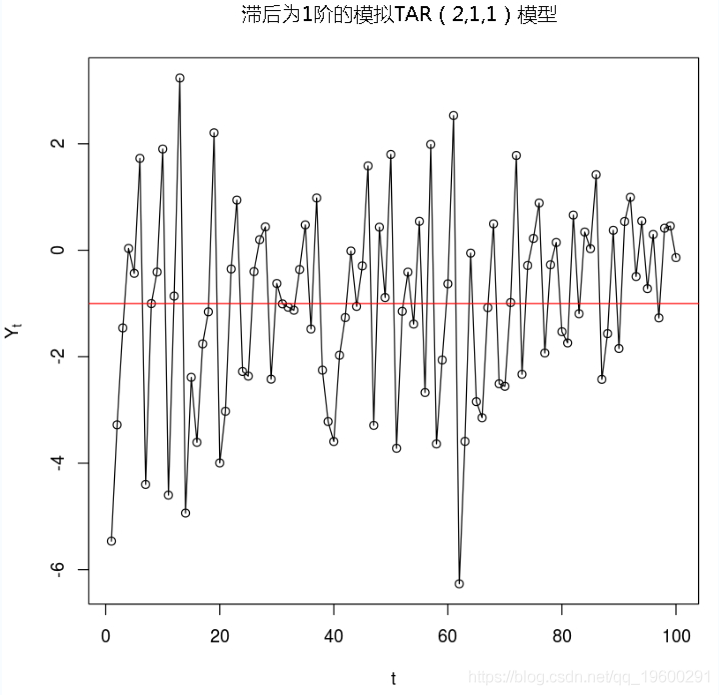
#模型估計數
sum( (lq <= y ) & (y <= uq) )80
如果d未知。
令d取值為1,2,3,...,p。為每個d的潛在值估算TAR模型,然后選擇殘差平方和最小的模型。
Chan(1993)已證明,CLS方法是一致的。
最小AIC(MAIC)方法
由于在實踐中這兩種情況的AR階數是未知的,因此需要一種允許對它們進行估計的方法。對于TAR模型,對于固定的r和d,AIC變為
![]()
然后,通過最小化AIC對象來估計參數,以便在某個時間間隔內搜索閾值參數,以使任何方案都有足夠的數據進行估計。
#估算模型
#如果知道閾值
#如果閾值尚不清楚
#MAIC 方法
for (d in 1:3) {
if (model.tar.s$AIC < AIC.best) {
AIC.best = model.tar.s$AIC
model.best$d = d
model.best$p1 = model.tar.s
ar.s$AIC, signif(model.tar.s$thd,4)
AICM| d | AIC | R | 1 | 2 |
|---|---|---|---|---|
| 1 | 311.2 | -1.0020 | 1 | 1 |
| 2 | 372.6 | 0.2218 | 1 | 2 |
| 3 | 388.4 | -1.3870 | 1 | 0 |
非線性測試
1.使用滯后回歸圖進行目測。
繪制Yt與其滯后。擬合的回歸曲線不是很直,可能表明存在非線性關系。
在[168]中:
lagplot(y)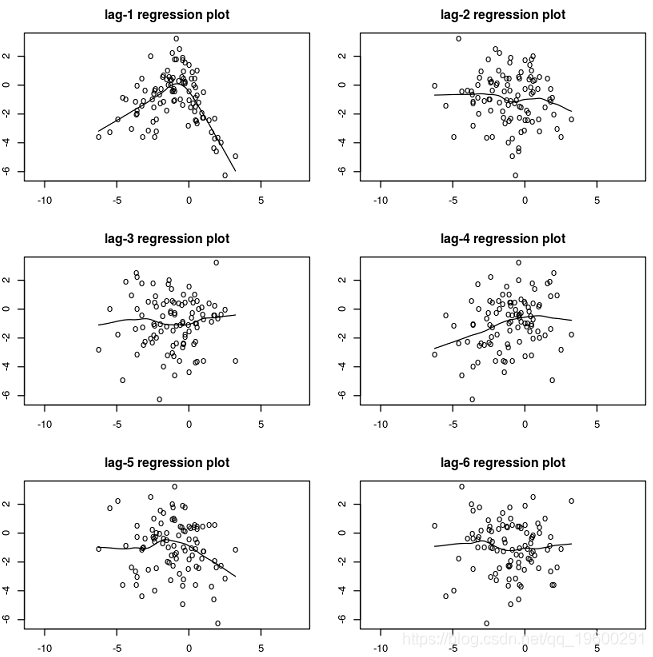
2.Keenan檢驗:
考慮以下由二階Volterra展開引起的模型:
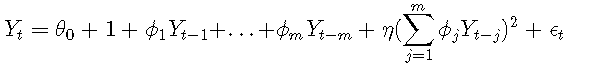
其中{ϵt} 的iid正態分布為零均值和有限方差。如果η=0,則該模型成為AR(mm)模型。
可以證明,Keenan檢驗等同于回歸模型中檢驗η=0:
![]()
其中Yt ^ 是從Yt-1,...,Yt-m上的Yt回歸得到的擬合值。
3. Tsay檢驗:
Keenan測試的一種更通用的替代方法。用更復雜的表達式替換為Keenan檢驗給出的上述模型中的項η(∑mj = 1ϕjYt-j)2。最后對所有非線性項是否均為零的二次回歸模型執行F檢驗。
在[169]中:
#檢查非線性: Keenan, Tsay
#Null is an AR model of order 1
Keenan.test(y,1)
$test.stat
90.2589565661567
$p.value
1.76111433596097e-15
$order
1在[170]中:
Tsay.test(y,1)
$test.stat
71.34
$p.value
3.201e-13
$order
14.檢驗閾值非線性
這是基于似然比的測試。
零假設是AR(pp)模型;另一種假設是具有恒定噪聲方差的p階的兩區域TAR模型,即σ1=σ2=σ。使用這些假設,可以將通用模型重寫為
![]()
零假設表明ϕ2,0 = ϕ2,1 = ... = ϕ2,p = 0。
似然比檢驗統計量可以證明等于
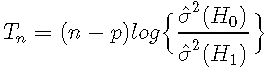
其中n-p是有效樣本大小,σ^ 2(H0)是線性AR(p)擬合的噪聲方差的MLE,而σ^ 2(H1)來自TAR的噪聲方差與在某個有限間隔內搜索到的閾值的MLE。
H0下似然比檢驗的采樣分布具有非標準采樣分布;參見Chan(1991)和Tong(1990)。
在[171]中:
res = tlrt(y, p=1, d=1, a=0.15, b=0.85)
res
$percentiles
14.1
85.9
$test.statistic
: 142.291963130459
$p.value
: 0模型診斷
使用殘差分析完成模型診斷。TAR模型的殘差定義為
![]()
標準化殘差是通過適當的標準偏差標準化的原始殘差:
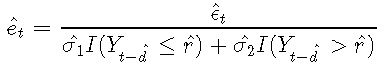
如果TAR模型是真正的數據機制,則標準化殘差圖應看起來是隨機的。可以通過檢查標準化殘差的樣本ACF來檢查標準化誤差的獨立性假設。
#模型診斷
diag(model.tar.best, gof.lag=20)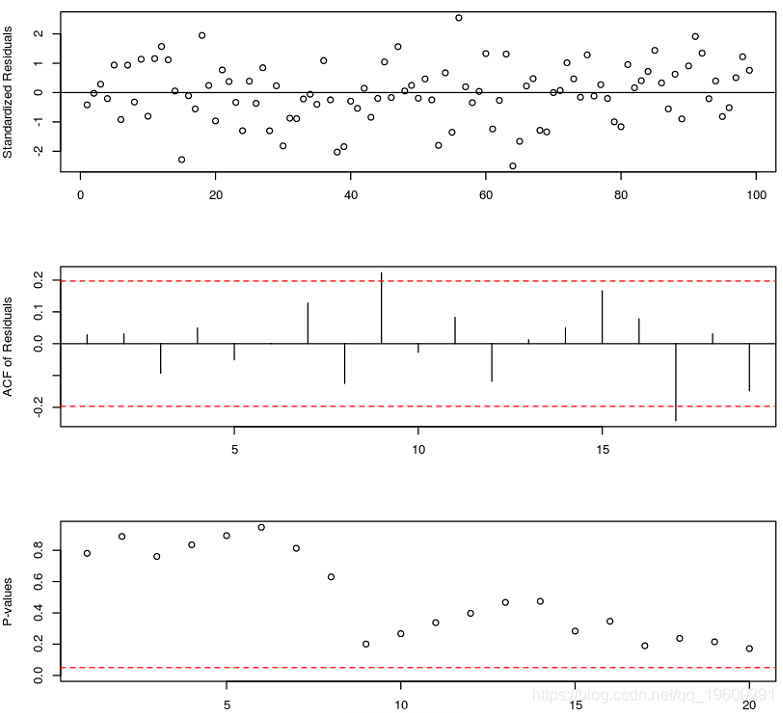
預測
預測分布通常是非正態的。通常,采用模擬方法進行預測。考慮模型
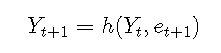
然后給定Yt = yt,Yt-1 = yt-1,...
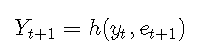
因此,可以通過從誤差分布中繪制et + 1并計算h(yt,et + 1),來獲得單步預測分布的Yt + 1的實現。 。
通過獨立重復此過程 B 次,您可以 從向前一步預測分布中隨機獲得B值樣本 。
可以通過這些B 值的樣本平均值來估計提前一步的預測平均值 。
通過迭代,可以輕松地將仿真方法擴展為找到任何l步提前預測分布:
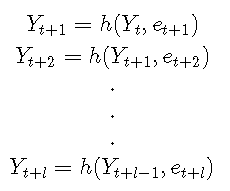
其中Yt = yt和et + 1,et + 2,...,et + l是從誤差分布得出的ll值的隨機樣本。
在[173]中:
#預測
model.tar.pred r.best, n.ahead = 10, n.sim=1000)
y.pred = ts(c
lines(ts(model.tar.pred$pred.interval[2,], start=end(y) + c(0,1), freq=1), lty=2)
lines(ts(model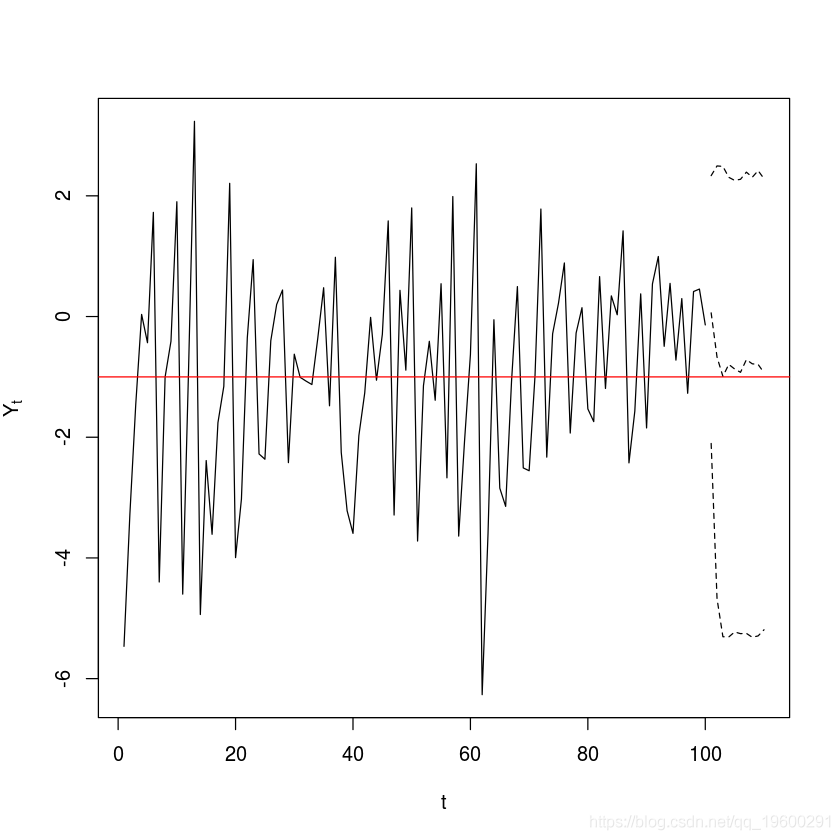
樣例
這里模擬的時間序列是1700年至1988年太陽黑子的年數量。
在[174]中:
#數據集
#太陽黑子序列,每年
plot.ts(sunsp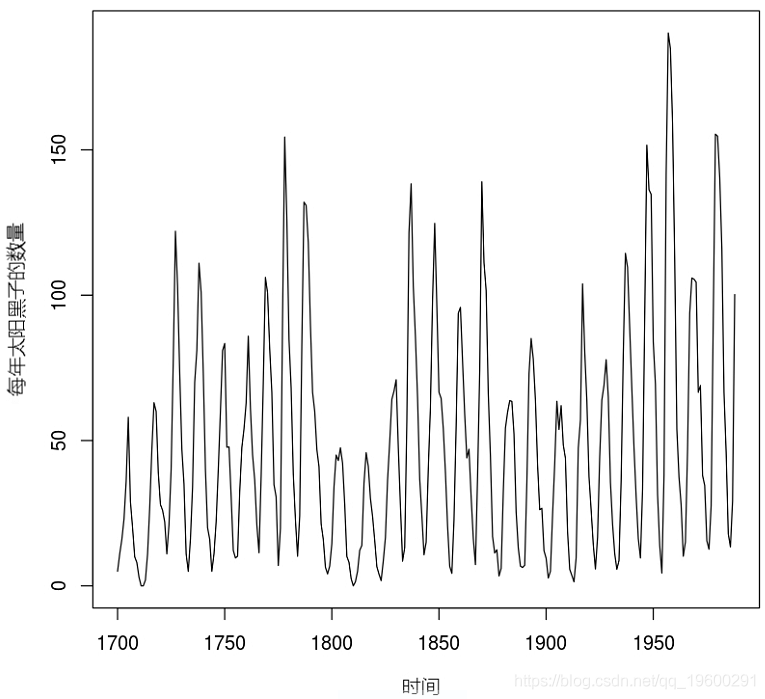
#通過滯后回歸圖檢查非線性
lagplot(sunspo)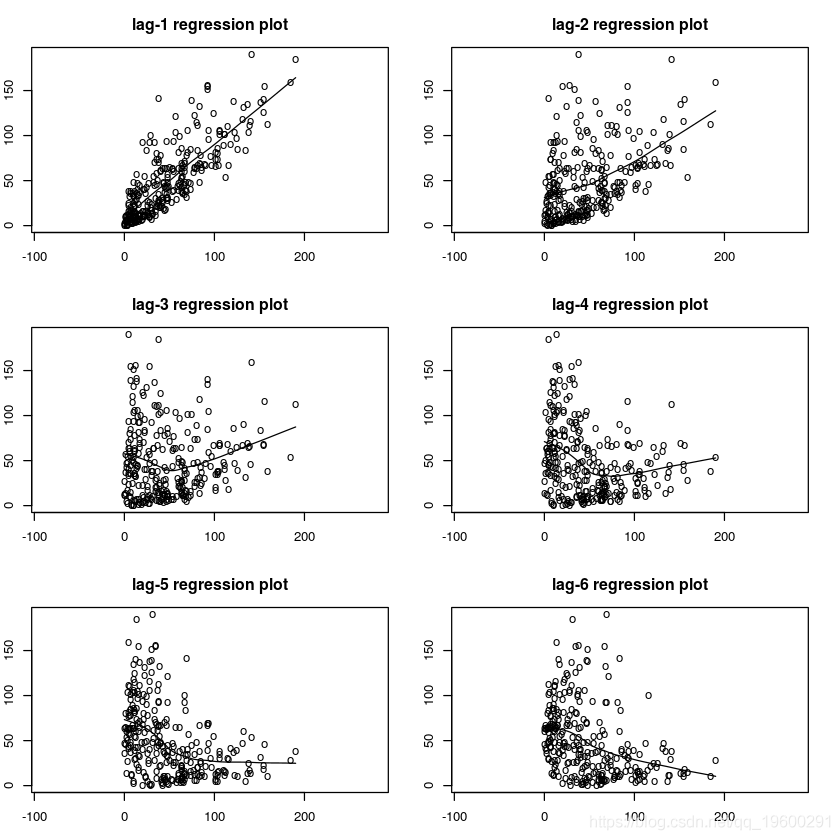
#使用假設檢驗檢查線性
Keenan.test(sunspot.year)
Tsay.test(sunspot.year)
$test.stat
18.2840758932705
$p.value
2.64565849317573e-05
$order
9
$test.stat
3.904
$p.value
6.689e-12
$order
9在[177]中:
#使用MAIC方法
AIC{
sunspot.tar.s = tar(sunspot.year, p1 = 9, p2 = 9, d = d, a=0.15, b=0.85)
AICM| d | AIC | R | 1 | 2 |
|---|---|---|---|---|
| 1 | 2285 | 22.7 | 6 | 9 |
| 2 | 2248 | 41.0 | 9 | 9 |
| 3 | 2226 | 31.5 | 7 | 9 |
| 4 | 2251 | 47.8 | 8 | 7 |
| 5 | 2296 | 84.8 | 9 | 3 |
| 6 | 2291 | 19.8 | 8 | 9 |
| 7 | 2272 | 43.9 | 9 | 9 |
| 8 | 2244 | 48.5 | 9 | 2 |
| 9 | 2221 | 47.5 | 9 | 3 |
在[178]中:
#測試閾值非線性
tl(sunspot.year, p=9, d=9, a=0.15, b=0.85)
$percentiles
15
85
$test.statistic
: 52.2571950943405
$p.value
: 6.8337179274236e-06
#模型診斷
tsdiag(sunspot.tar.best)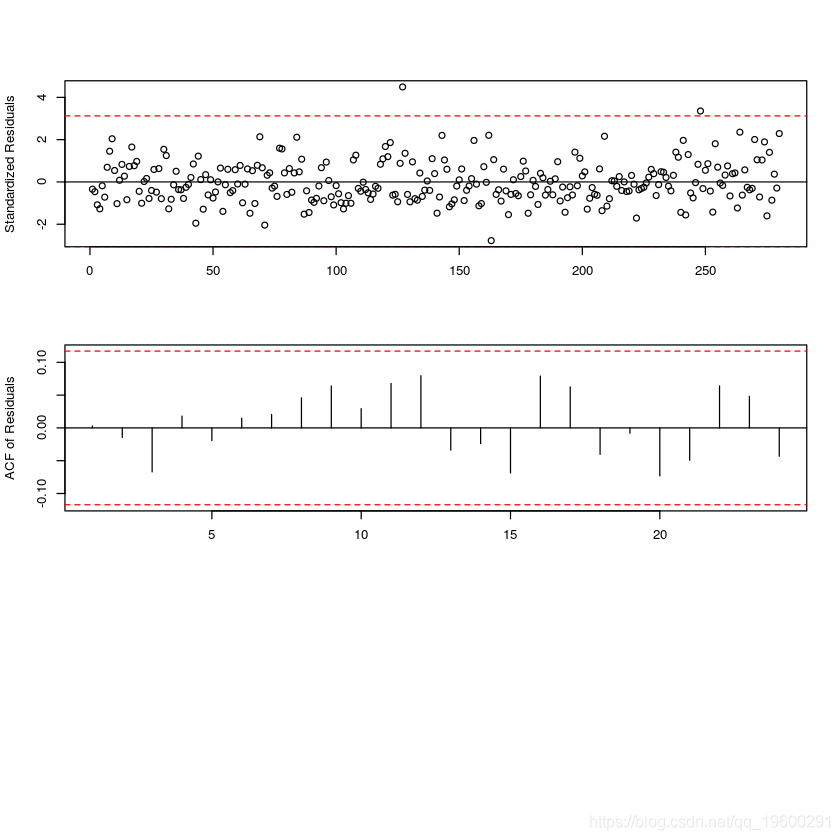
#預測
sunspot.tar.pred <- predict(sunspot.tar.best, n.ahead = 10, n.sim=1000)
lines(ts(sunspot.tar.pred$pretart=e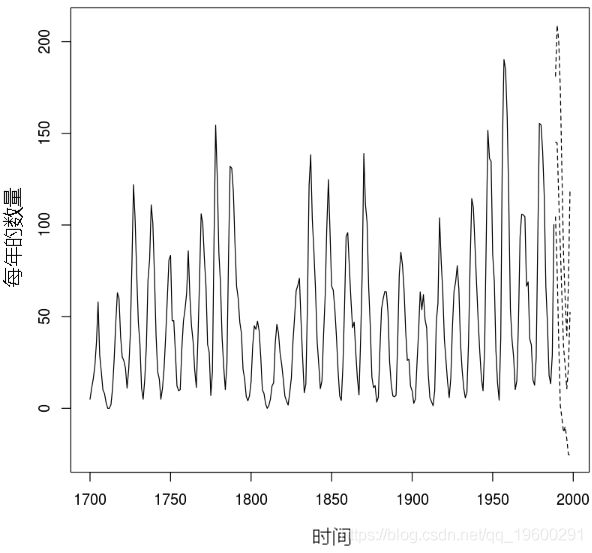
#擬合線性AR模型
#pacf(sunspot.year)
#嘗試AR階數9
ord = 9
ar.mod <- arima(sunspot.year, order=c(ord,0,0), method="CSS-ML")
plot.ts(sunspot.year[10:289]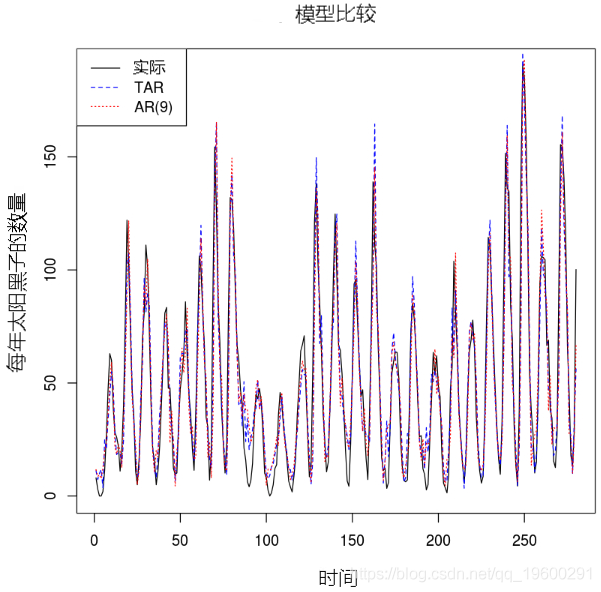
模擬TAR模型上的AR性能
示例1. 將AR(4)擬合到TAR模型
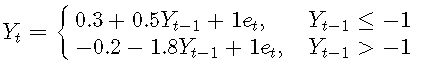
set.seed(12349)
#低機制參數
i1 = 0.3
p1 = 0.5
s1 = 1
#高機制參數
i2 = -0.2
p2 = -1.8
s2 = 1
thresh = -1
delay = 1
nobs = 200
#模擬200個樣本
y=sim(n=nobs,Phi1=c(i1,p1),Phi$y
#使用Tsay的檢驗確定最佳AR階數
ord <- Tsay.test(y)$order
#線性AR模型
#pacf(sunspot.year)
#try AR order 4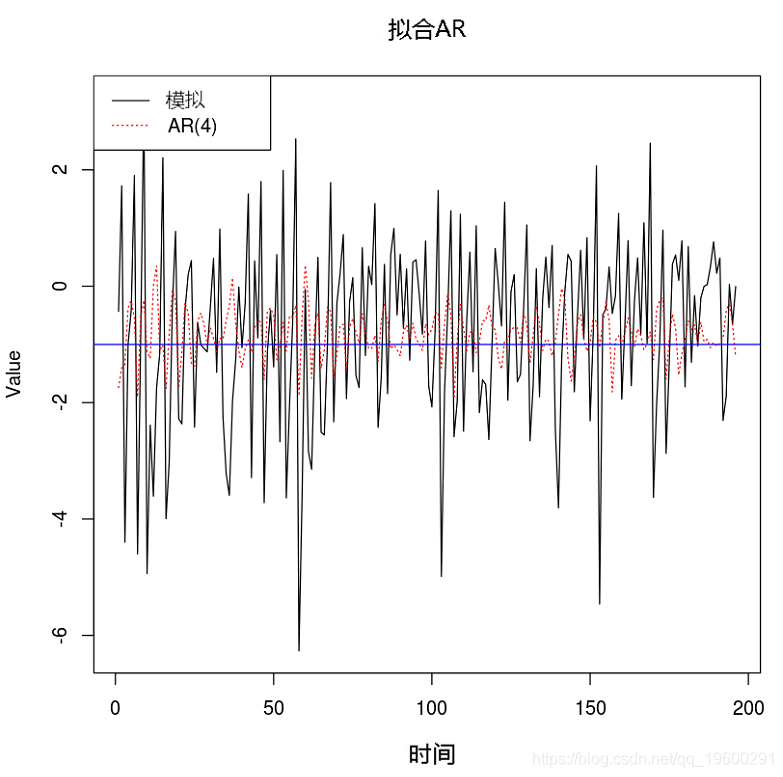
例子2. 將AR(4)擬合到TAR模型
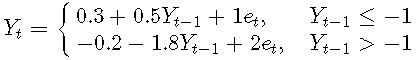
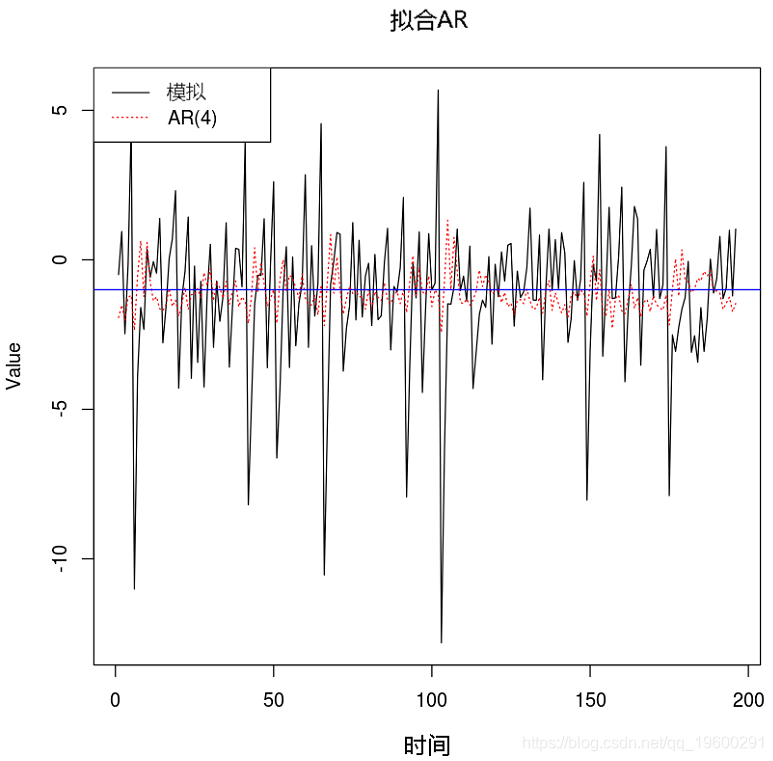
例子3. 將AR(3)擬合到TAR模型
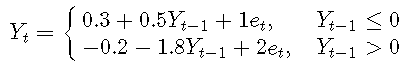
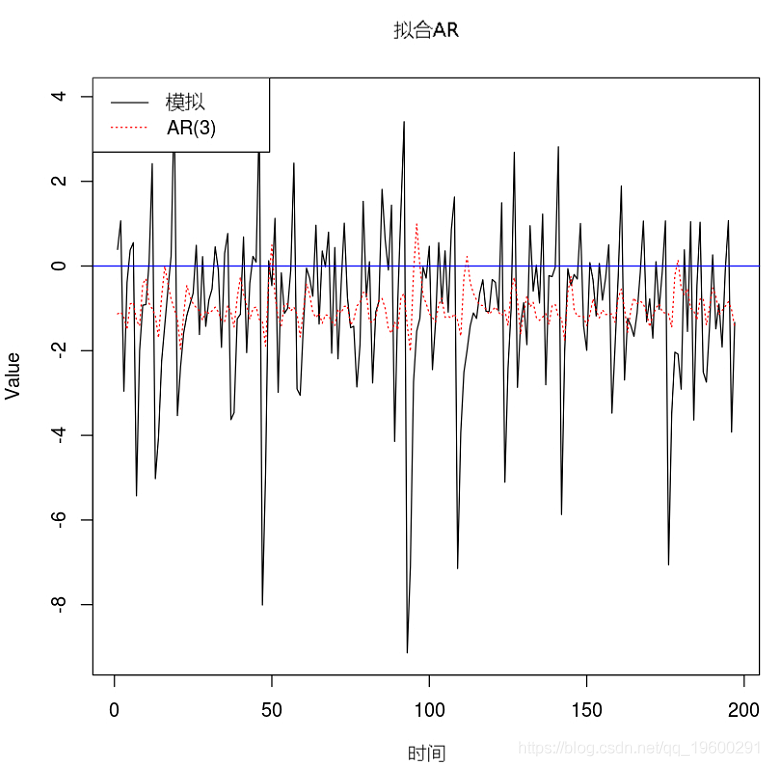
例子3. 將AR(7)擬合到TAR模型
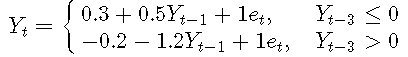
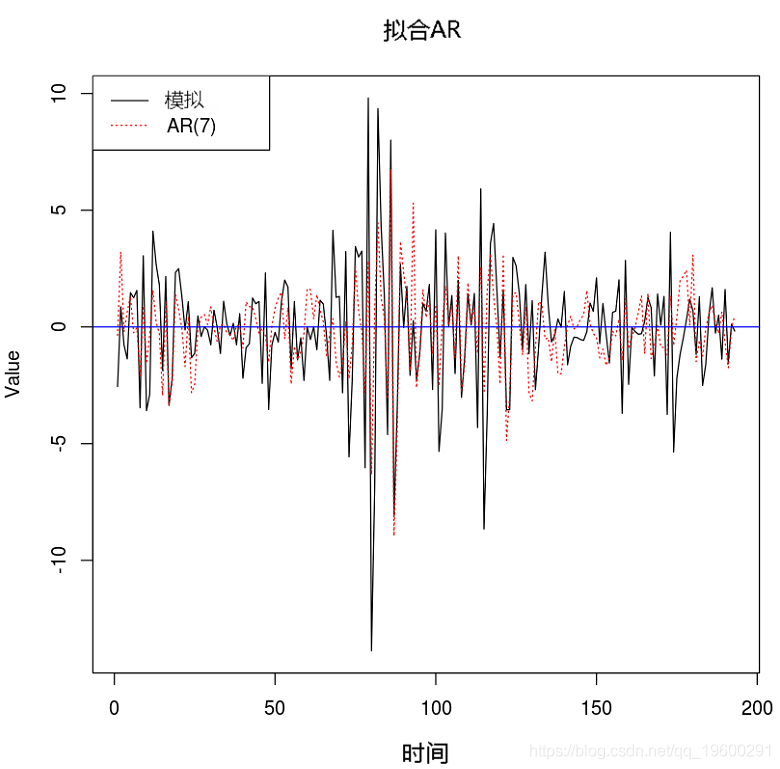
參考文獻
恩德斯(W. Enders),2010年。應用計量經濟學時間序列

到此這篇關于R語言時間序列TAR閾值自回歸模型示例詳解的文章就介紹到這了,更多相關R語言時間序列內容請搜索html5模板網以前的文章希望大家以后多多支持html5模板網!
