在標準線性模型中,我們假設 ![]() 。當線性假設無法滿足時,可以考慮使用其他方法。
。當線性假設無法滿足時,可以考慮使用其他方法。
多項式回歸
擴展可能是假設某些多項式函數,
![]()
同樣,在標準線性模型方法(使用GLM的條件正態分布)中,參數 ![]() 可以使用最小二乘法獲得,其中
可以使用最小二乘法獲得,其中 ![]() 在
在 ![]() 。
。
即使此多項式模型不是真正的多項式模型,也可能仍然是一個很好的近似值 ![]() 。實際上,根據 Stone-Weierstrass定理,如果
。實際上,根據 Stone-Weierstrass定理,如果 ![]() 在某個區間上是連續的,則有一個統一的近似值
在某個區間上是連續的,則有一個統一的近似值 ![]() ,通過多項式函數。
,通過多項式函數。
僅作說明,請考慮以下數據集
db = data.frame(x=xr,y=yr)
plot(db)
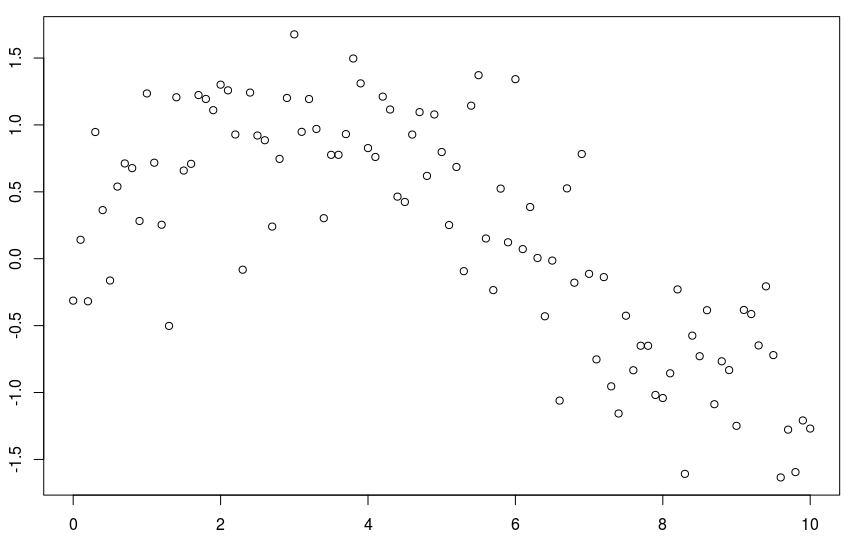
與標準回歸線
reg = lm(y ~ x,data=db)
abline(reg,col="red")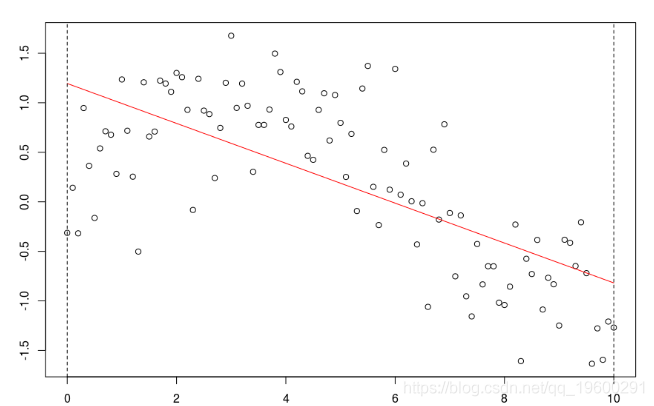
考慮一些多項式回歸。如果多項式函數的次數足夠大,則可以獲得任何一種模型,
reg=lm(y~poly(x,5),data=db)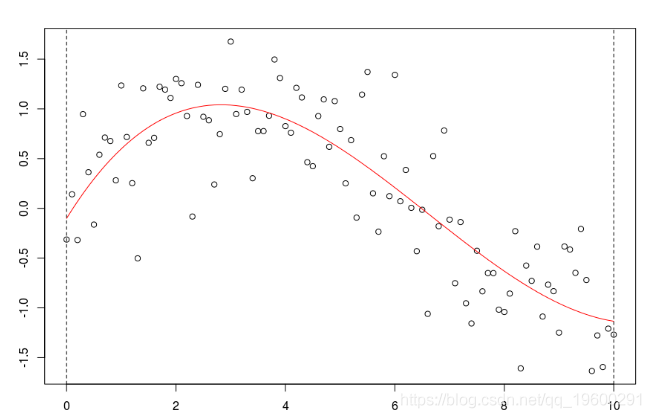
但是,如果次數太大,那么會獲得太多的“波動”,
reg=lm(y~poly(x,25),data=db)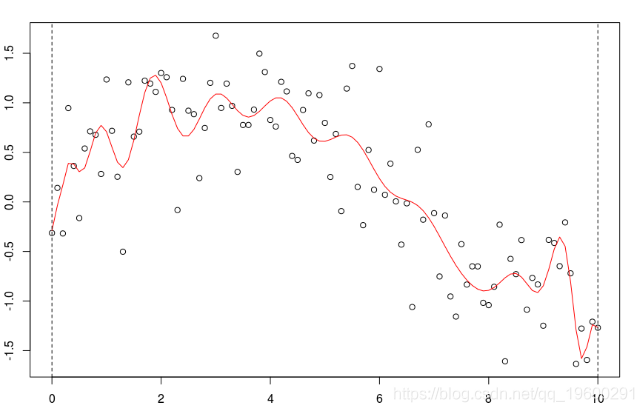
并且估計值可能不可靠:如果我們更改一個點,則可能會發生(局部)更改
yrm=yr;yrm[31]=yr[31]-2
lines(xr,predict(regm),col="red")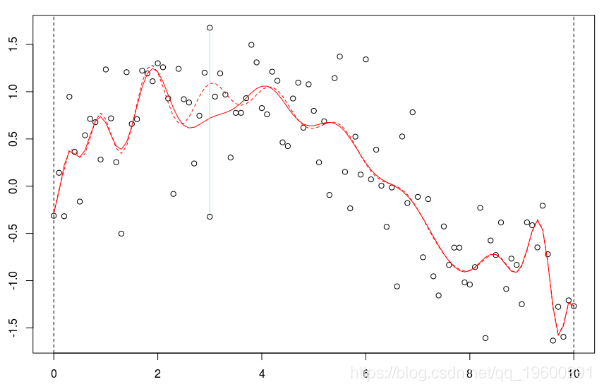
局部回歸
實際上,如果我們的興趣是局部有一個很好的近似值 ![]() ,為什么不使用局部回歸?
,為什么不使用局部回歸?
使用加權回歸可以很容易地做到這一點,在最小二乘公式中,我們考慮
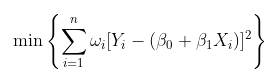
在這里,我考慮了線性模型,但是可以考慮任何多項式模型。在這種情況下,優化問題是
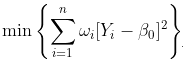 可以解決,因為
可以解決,因為
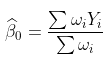
例如,如果我們想在某個時候進行預測 , 考慮 ![]() 。使用此模型,我們可以刪除太遠的觀測值,
。使用此模型,我們可以刪除太遠的觀測值,
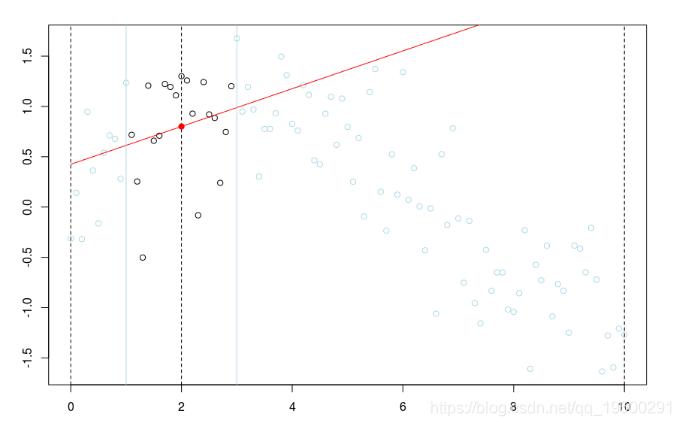
更一般的想法是考慮一些核函數 ![]() 給出權重函數,以及給出鄰域長度的一些帶寬(通常表示為h),
給出權重函數,以及給出鄰域長度的一些帶寬(通常表示為h),
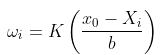
這實際上就是所謂的 Nadaraya-Watson 函數估計器 ![]() 。
。
在前面的案例中,我們考慮了統一核 ![]() ,
,
但是使用這種權重函數具有很強的不連續性不是最好的選擇,嘗試高斯核,
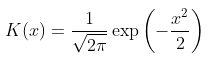
這可以使用
w=dnorm((xr-x0))
reg=lm(y~1,data=db,weights=w)在我們的數據集上,我們可以繪制
w=dnorm((xr-x0))
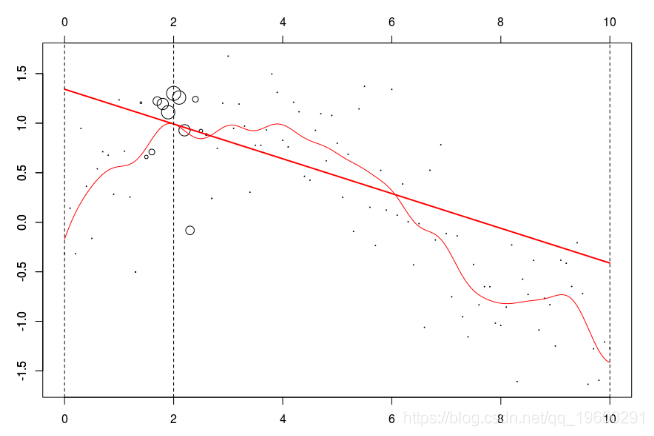
plot(db,cex=abs(w)*4)
lines(ul,vl0,col="red")
axis(3)
axis(2)
reg=lm(y~1,data=db,weights=w)
u=seq(0,10,by=.02)
v=predict(reg,newdata=data.frame(x=u))
lines(u,v,col="red",lwd=2)在這里,我們需要在點2進行局部回歸。下面的水平線是回歸(點的大小與寬度成比例)。紅色曲線是局部回歸的演變
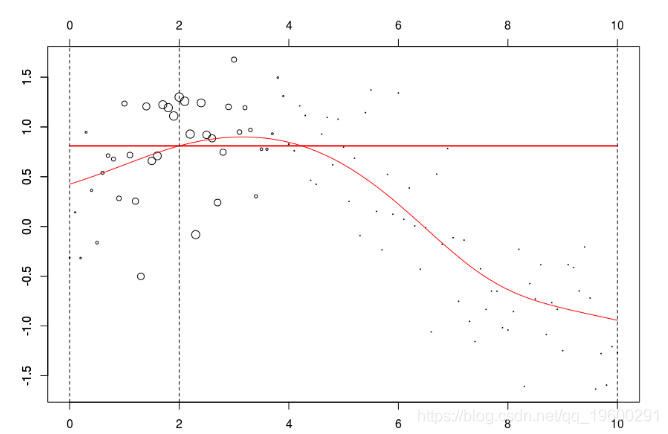
讓我們使用動畫來可視化曲線。
但是由于某些原因,我無法在Linux上輕松安裝該軟件包。我們可以使用循環來生成一些圖形
name=paste("local-reg-",100+i,".png",sep="")
png(name,600,400)
for(i in 1:length(vx0)) graph (i)然后,我使用

當然,可以考慮局部線性模型,
return(predict(reg,newdata=data.frame(x=x0)))}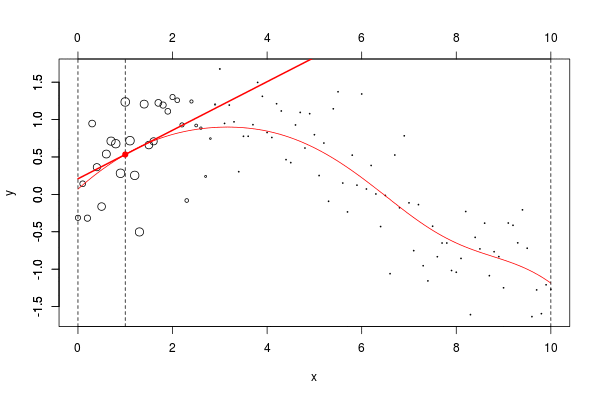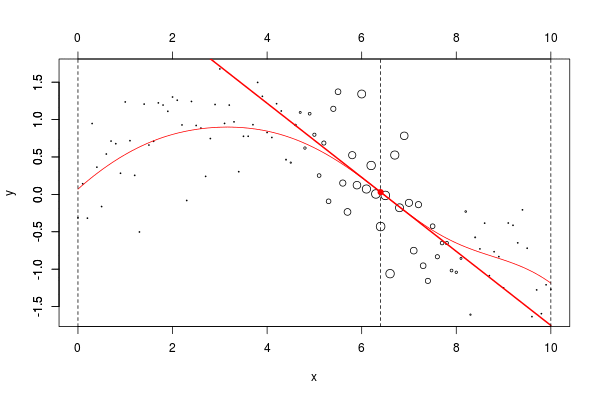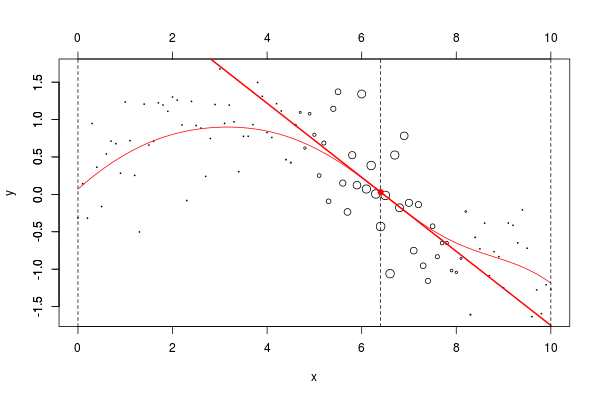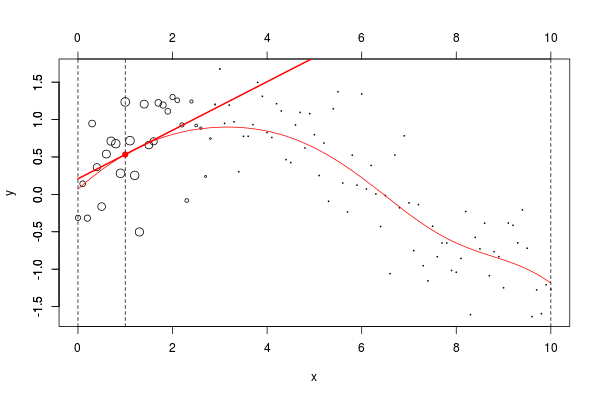
甚至是二次(局部)回歸,
lm(y~poly(x,degree=2), weights=w)
當然,我們可以更改帶寬
請注意,實際上,我們必須選擇權重函數(所謂的核)。但是,有(簡單)方法來選擇“最佳”帶寬h。交叉驗證的想法是考慮
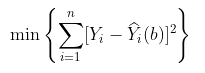
![]() 是使用局部回歸獲得的預測。
是使用局部回歸獲得的預測。
我們可以嘗試一些真實的數據。
library(XML)
data = readHTMLTable(html)整理數據集,
plot(data$no,data$mu,ylim=c(6,10))
segments(data$no,data$mu-1.96*data$se,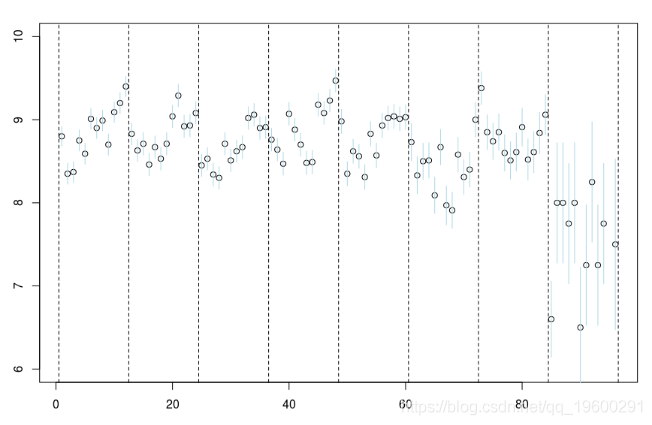
我們計算標準誤差,反映不確定性。
for(s in 1:8){reg=lm(mu~no,data=db,
lines((s predict(reg)[1:12]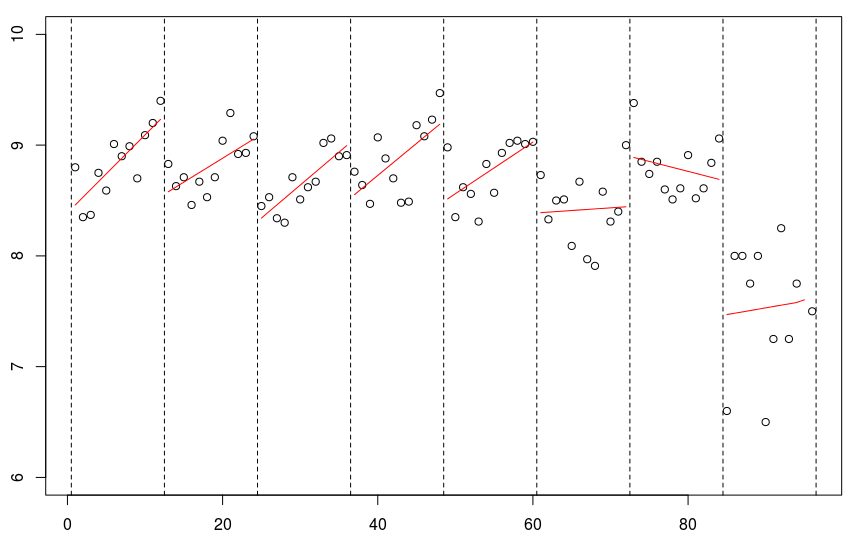
所有季節都應該被認為是完全獨立的,這不是一個很好的假設。
smooth(db$no,db$mu,kernel = "normal",band=5)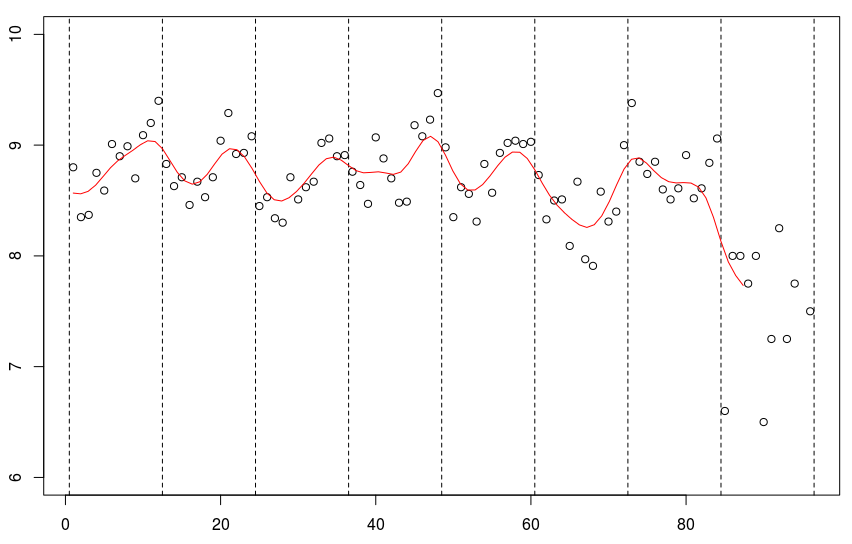
我們可以嘗試查看帶寬較大的曲線。
db$mu[95]=7
plot(data$no,data$mu
lines(NW,col="red")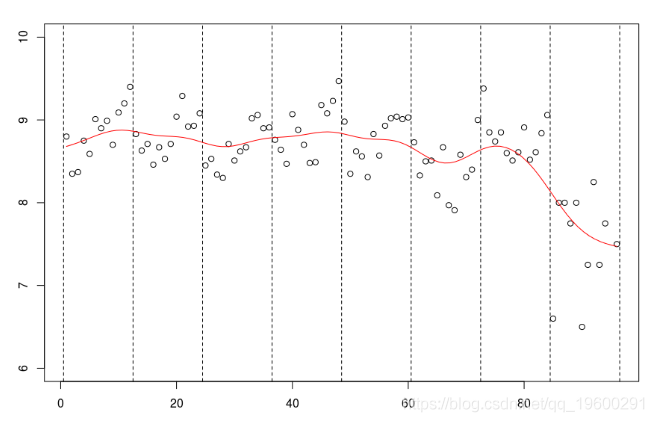
樣條平滑
接下來,討論回歸中的平滑方法。假設![]() ,
, ![]() 是一些未知函數,但假定足夠平滑。例如,假設
是一些未知函數,但假定足夠平滑。例如,假設 ![]() 是連續的,
是連續的, ![]() 存在,并且是連續的,
存在,并且是連續的, ![]() 存在并且也是連續的等等。如果
存在并且也是連續的等等。如果 ![]() 足夠平滑, 可以使用泰勒展開式。 因此,對于
足夠平滑, 可以使用泰勒展開式。 因此,對于 ![]()
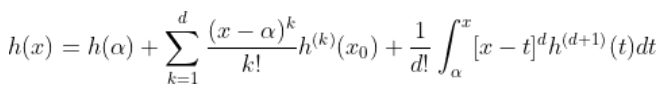
也可以寫成
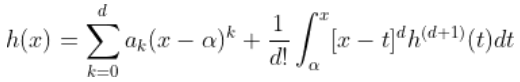
第一部分只是一個多項式。
使用 黎曼積分,觀察到
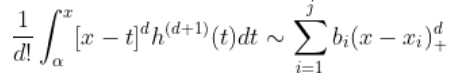
因此,
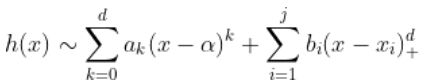
我們有線性回歸模型。一個自然的想法是考慮回歸 

![]()
給一些節點 
plot(db)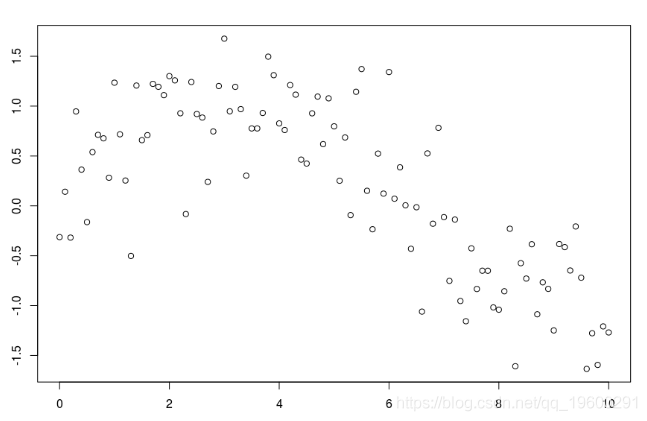
如果我們考慮一個節點,并擴展階數1,
B=bs(xr,knots=c(3),Boundary.knots=c(0,10),degre=1)
lines(xr[xr<=3],predict(reg)[xr<=3],col="red")
lines(xr[xr>=3],predict(reg)[xr>=3],col="blue")可以將用該樣條獲得的預測與子集(虛線)上的回歸進行比較。
lines(xr[xr<=3],predict(reg)[xr<=3
lm(yr~xr,subset=xr>=3)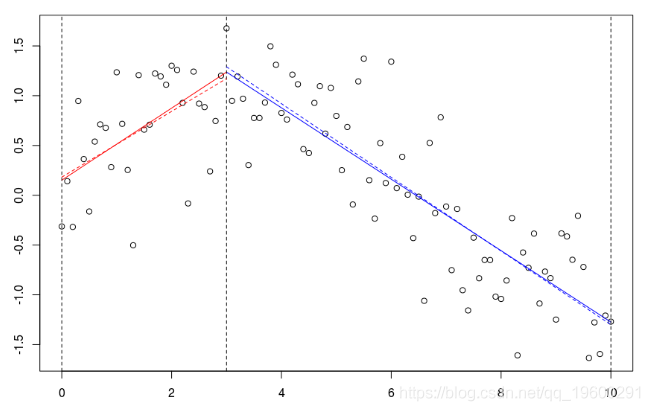
這是不同的,因為這里我們有三個參數(關于兩個子集的回歸)。當要求連續模型時,失去了一個自由度。觀察到可以等效地寫
lm(yr~bs(xr,knots=c(3),Boundary.knots=c(0,10)回歸中出現的函數如下
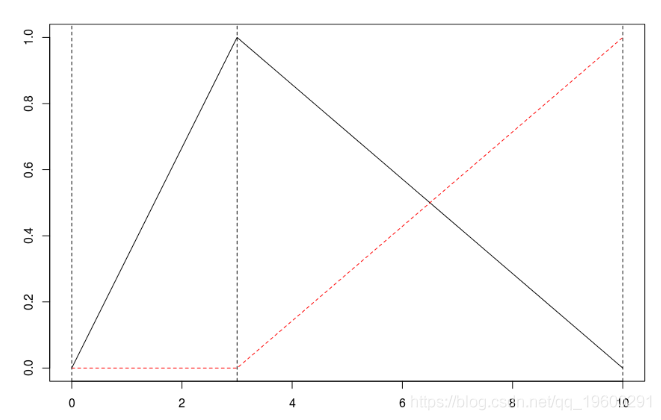
現在,如果我們對這兩個分量進行回歸,我們得到
matplot(xr,B
abline(v=c(0,2,5,10),lty=2)如果加一個節點,我們得到
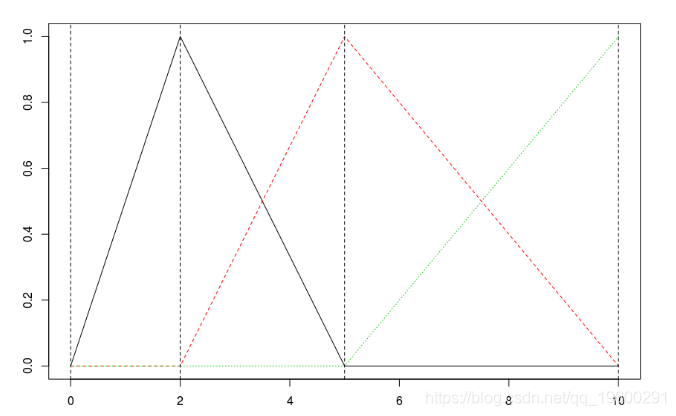
預測是
lines(xr,predict(reg),col="red")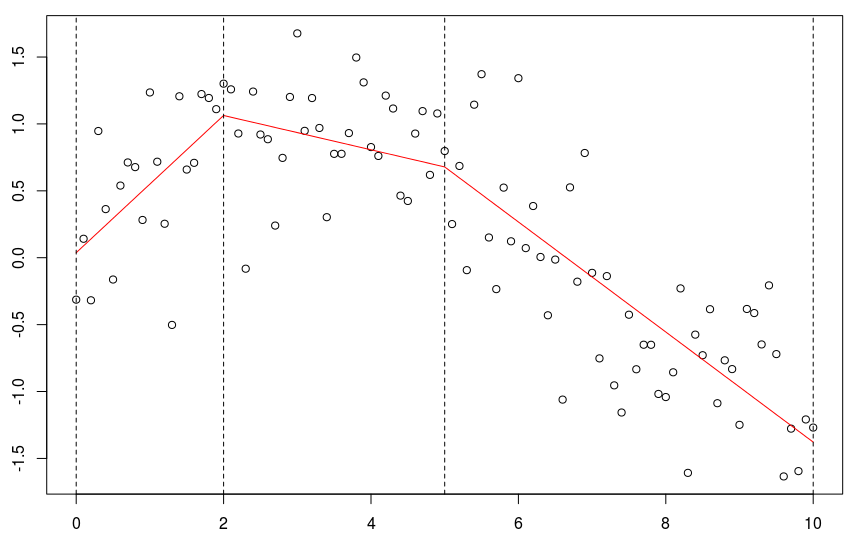
我們可以選擇更多的節點
lines(xr,predict(reg),col="red")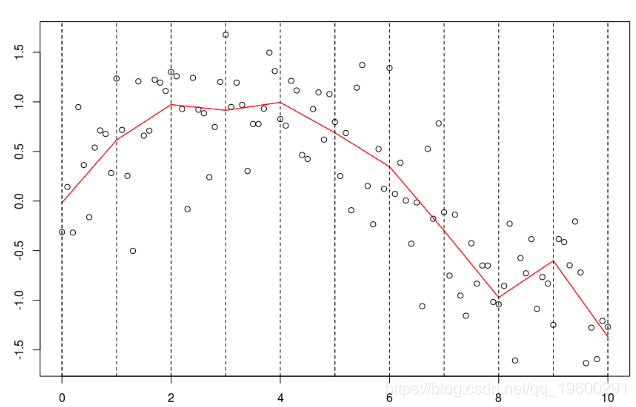
我們可以得到一個置信區間
polygon(c(xr,rev(xr)),c(P[,2],rev(P[,3]))
points(db)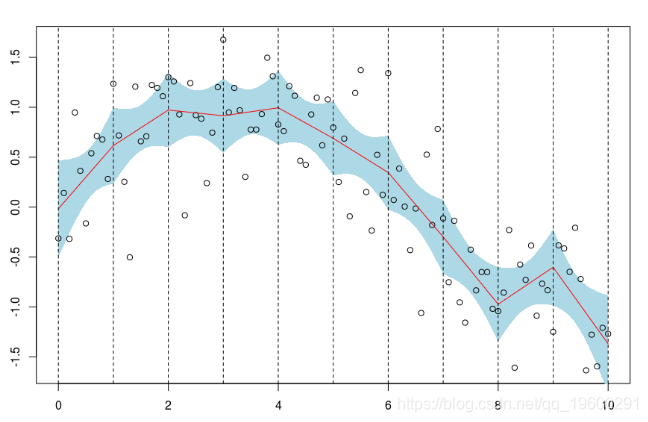
如果我們保持先前選擇的兩個節點,但考慮泰勒的2階的展開,我們得到
matplot(xr,B,type="l")
abline(v=c(0,2,5,10),lty=2)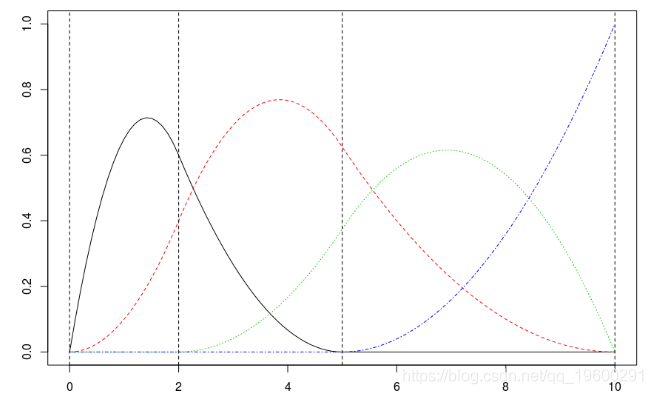
如果我們考慮常數和基于樣條的第一部分,我們得到
B=cbind(1,B)
lines(xr,B[,1:k]%*%coefficients(reg)[1:k],col=k-1,lty=k-1)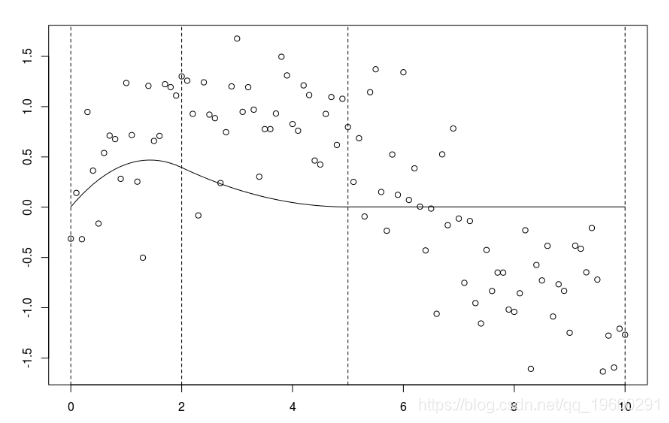
如果我們將常數項,第一項和第二項相加,則我們得到的部分在第一個節點之前位于左側,
k=3
lines(xr,B[,1:k]%*%coefficients(reg)[1:k]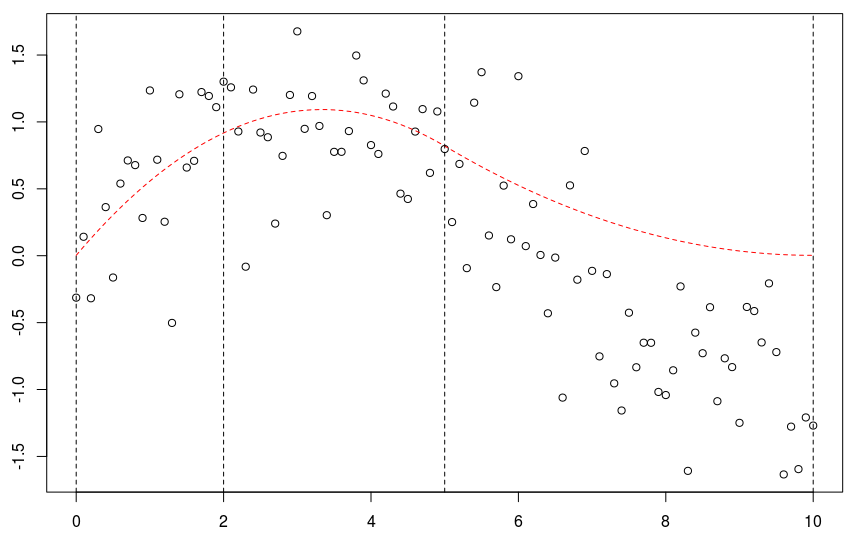
通過基于樣條的矩陣中的三個項,我們可以得到兩個節點之間的部分,
lines(xr,B[,1:k]%*%coefficients(reg)[1:k]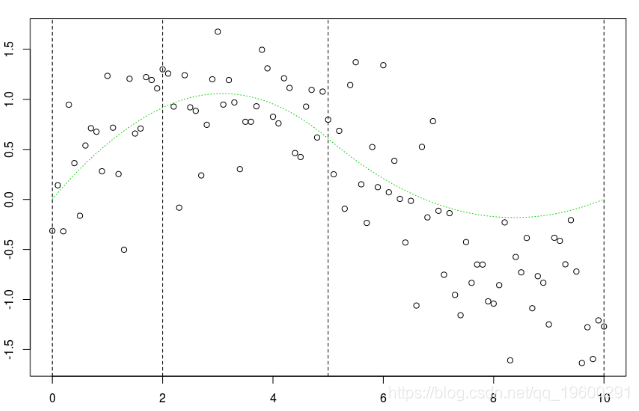
最后,當我們對它們求和時,這次是最后一個節點之后的右側部分,
k=5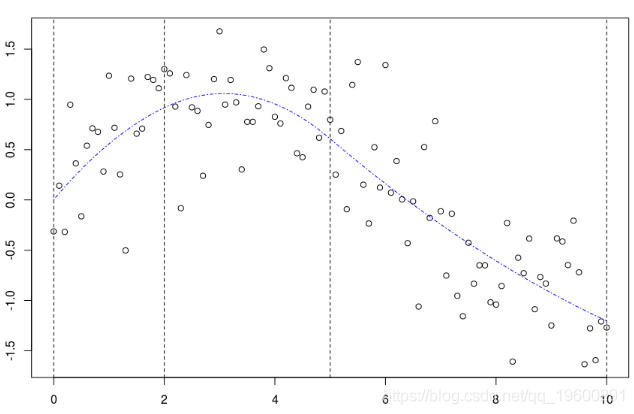
這是我們使用帶有兩個(固定)節點的二次樣條回歸得到的結果。可以像以前一樣獲得置信區間
polygon(c(xr,rev(xr)),c(P[,2],rev(P[,3]))
points(db)
lines(xr,P[,1],col="red")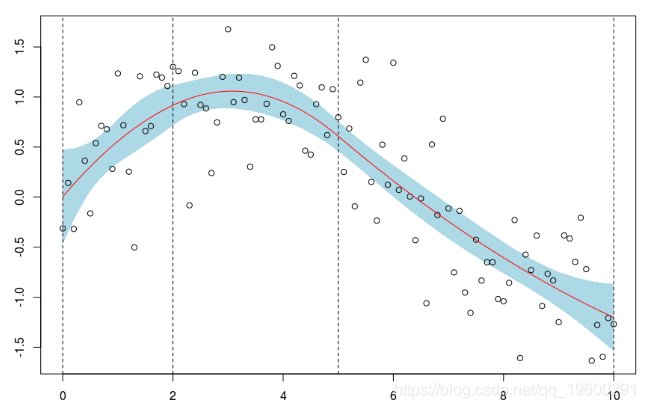
使用函數 

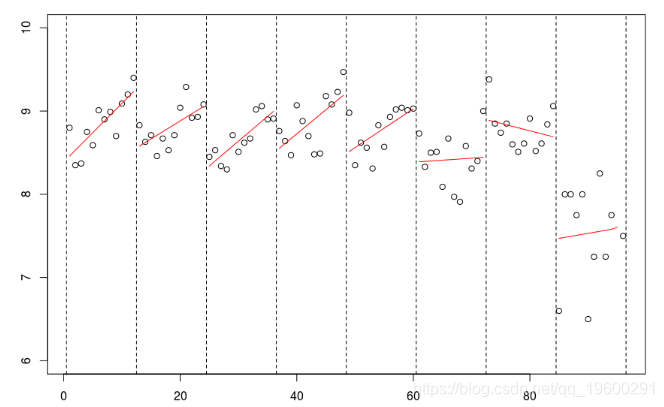
再一次,使用線性樣條函數,可以增加連續性約束,
lm(mu~bs(no,knots=c(12*(1:7)+.5),Boundary.knots=c(0,97),
lines(c(1:94,96),predict(reg),col="red")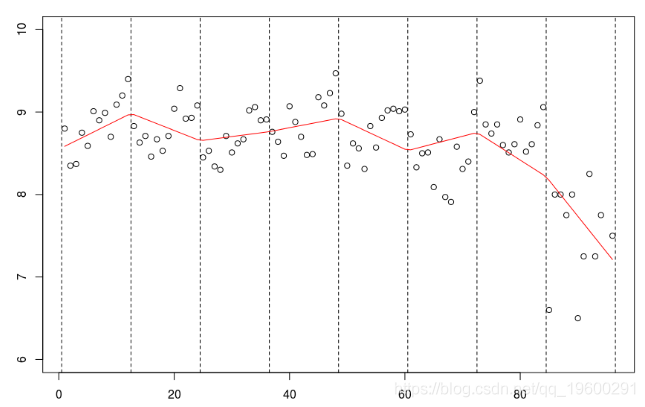
但是我們也可以考慮二次樣條,
abline(v=12*(0:8)+.5,lty=2)
lm(mu~bs(no,knots=c(12*(1:7)+.5),Boundary.knots=c(0,97),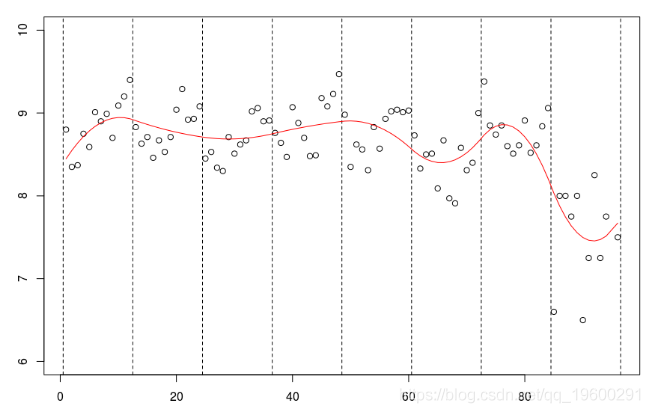

到此這篇關于詳解R語言中的多項式回歸、局部回歸、核平滑和平滑樣條回歸模型的文章就介紹到這了,更多相關R語言多項式回歸、局部回歸內容請搜索html5模板網以前的文章希望大家以后多多支持html5模板網!
